Ozancan Ozdemir - ozancan@metu.edu.tr
This document is created using the following sources.
Reminder
import numpy as np # import the numpy package
a = np.array([1, 2, 3]) # Create a rank 1 array (1D array)
a
array([1, 2, 3])
type(a)
numpy.ndarray
b = np.array([[1,2,3],[4,5,6]]) #Create 2D array
b
array([[1, 2, 3],
[4, 5, 6]])
np.mean(b)
3.5
What makes working with numpy so powerful and convenient is that it
comes with many vectorized math functions for computation over
elements of an array. These functions are highly optimized and are
very fast - much, much faster than using an explicit for loop.
For example, let’s create a large array of random values and then sum it
both ways. We’ll use a %%time cell magic to time them.
a = np.random.random(100000000)
%%time
x = np.sum(a)
CPU times: user 72.4 ms, sys: 0 ns, total: 72.4 ms Wall time: 73.8 ms
%%time
x = 0
for element in a:
x = x + element
CPU times: user 15.9 s, sys: 36.2 ms, total: 15.9 s Wall time: 16 s
Look at the “Wall Time” in the output - note how much faster the vectorized version of the operation is! This type of fast computation is a major enabler of machine learning, which requires a lot of computation.
Whenever possible, we will try to use these vectorized operations.
Some mathematic functions are available both as operator overloads and as functions in the numpy module.
For example, you can perform an elementwise sum on two arrays using
either the + operator or the add() function.
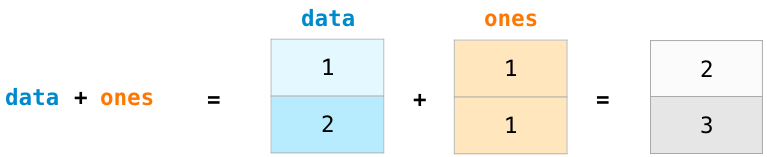
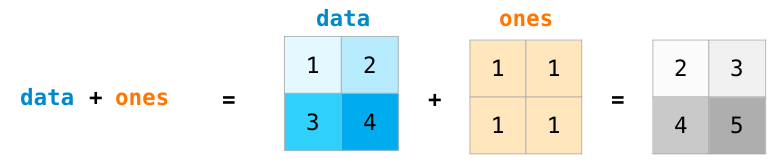
x = np.array([[1,2],[3,4]], dtype=np.float64)
y = np.array([[5,6],[7,8]], dtype=np.float64)
# Elementwise sum; both produce the array
print(x + y)
print(np.add(x, y))
[[ 6. 8.] [10. 12.]] [[ 6. 8.] [10. 12.]]
And this works for other operations as well, not only addition:

# Elementwise difference; both produce the array
print(x - y)
print(np.subtract(x, y))
[[-4. -4.] [-4. -4.]] [[-4. -4.] [-4. -4.]]
# Elementwise product; both produce the array
print(x * y)
print(np.multiply(x, y))
[[ 5. 12.] [21. 32.]] [[ 5. 12.] [21. 32.]]
# Elementwise division; both produce the array
# [[ 0.2 0.33333333]
# [ 0.42857143 0.5 ]]
print(x / y)
print(np.divide(x, y))
[[0.2 0.33333333] [0.42857143 0.5 ]] [[0.2 0.33333333] [0.42857143 0.5 ]]
# Elementwise square root; produces the array
# [[ 1. 1.41421356]
# [ 1.73205081 2. ]]
print(np.sqrt(x))
[[1. 1.41421356] [1.73205081 2. ]]
# Elementwise exponential power; produces array
#[[ 2.71828183 7.3890561 ]
#[20.08553692 54.59815003]]
print(np.exp(x))
[[ 2.71828183 7.3890561 ] [20.08553692 54.59815003]]
np.round(np.exp(x)) #Round an array to the given number of decimals.;elementwise
array([[ 3., 7.],
[20., 55.]])
np.ceil(np.exp(x)) #Return the ceiling of the input, element-wise.
array([[ 3., 8.],
[21., 55.]])
np.floor(np.exp(x)) #Return the floor of the input, element-wise.
array([[ 2., 7.],
[20., 54.]])
You can find out more functions from here.
Note that * operator is not a matrix multipication operator in contrast to other programming languages like MATLAB. dot() function instead is used to compute inner products of vectors, to multiply a vector by a matrix, and to multiply matrices. dot() is available both as a function in the numpy module
and as an instance method of array objects:

import numpy as np
x = np.array([[1,2],[3,4]])
y = np.array([[5,6],[7,8]])
v = np.array([9,10])
w = np.array([11, 12])
print(x)
print(y)
print(v)
print(w)
[[1 2] [3 4]] [[5 6] [7 8]] [ 9 10] [11 12]
# Inner product of vectors; both produce 219
print(v.dot(w))
print(np.dot(v, w))
219 219
You can also use the @ operator which is equivalent to numpy's dot
operator.
print(v @ w)
219
Multiply a 5x3 matrix by a 3x2 matrix (real matrix product) where the all elements in both matrices are 1.
Hint: Use np.ones()
The Expected Output:
m1 = np.ones((5,3))
m1
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
m2 = np.ones((3,2))
m2
array([[1., 1.],
[1., 1.],
[1., 1.]])
m1@m2
array([[3., 3.],
[3., 3.],
[3., 3.],
[3., 3.],
[3., 3.]])
Numpy also provides many useful functions for performing computations on arrays, such as min(), max(), sum(),mean(),median(), quantile(), cov(), corrcoef(),and others:
You can see the full list for the mathematical functions from here and statistical functions from here

x = np.array([[1, 2], [3, 4], [5, 6]])
print(x)
[[1 2] [3 4] [5 6]]
print(np.min(x)) # Show min of all elements; prints "1"
1
print(np.max(x)) # Show max of all elements; prints "6"
6
print(np.mean(x)) # Compute the mean of the all elements; prints "3.5"
3.5
$\frac{\sum_{i=1}^{n=6} i}{6} = 3.5$
print(np.median(x)) # Compute the median of the all elements; prints "3.5"
3.5
print(np.quantile(x, 0.75)) # Compute the 3rd quartile of the all elements; prints "4.75"
4.75
print(np.std(x)) # Compute the standard deviation of the all elements; prints "1.708"
1.707825127659933
print(np.sum(x)) # Compute sum of all elements; prints "21"
21
print(np.cumsum(x)) # Compute cumulative sum of all elements; prints "21"
[ 1 3 6 10 15 21]
Now, let's see how the correlating function works.
a = np.array([0.45959958, 0.1613048 , 0.76000473, 0.07536241, 0.60232491,
0.00167602, 0.71653501, 0.40927931, 0.78030462, 0.15509362])
b = np.array([7.17485455, 5.50089164, 7.35266241, 5.64972889, 7.62871573,
5.01298309, 7.57177999, 6.81378627, 7.3785654 , 5.79279215])
np.cov(a,b)
array([[0.08872592, 0.28013513],
[0.28013513, 0.98124247]])
np.corrcoef(a,b)
array([[1. , 0.94941078],
[0.94941078, 1. ]])
Not only can we aggregate all the values in a matrix using these
functions, but we can also aggregate across the rows or columns by using
the axis parameter:

x = np.array([[1, 2], [5, 3], [4, 6]])
print(np.max(x, axis=0)) # Compute max of each column; prints "[5 6]"
[5 6]
print(np.max(x, axis=1)) # Compute max of each row; prints "[2 5 6]"
[2 5 6]
print(np.mean(x, axis=1)) # Compute mean of each row; prints "[1.5 4 5]"
[1.5 4. 5. ]
np.sort returns the sorted copy of the array.
a
array([0.45959958, 0.1613048 , 0.76000473, 0.07536241, 0.60232491,
0.00167602, 0.71653501, 0.40927931, 0.78030462, 0.15509362])
np.sort(a) #from smallest to largest
array([0.00167602, 0.07536241, 0.15509362, 0.1613048 , 0.40927931,
0.45959958, 0.60232491, 0.71653501, 0.76000473, 0.78030462])
np.sort(a)[::-1] #from largest to smallest
array([0.78030462, 0.76000473, 0.71653501, 0.60232491, 0.45959958,
0.40927931, 0.1613048 , 0.15509362, 0.07536241, 0.00167602])
Extra
You can generate order your data in a random order.
np.random.shuffle(a)
a
array([0.00167602, 0.60232491, 0.45959958, 0.71653501, 0.15509362,
0.40927931, 0.78030462, 0.07536241, 0.1613048 , 0.76000473])
Create a 1D array having 10 elements. You can use .random function.
Calculate the five number summaries of the array.
Answer:
ex2 = np.random.random(10)
ex2
array([0.06354225, 0.25978659, 0.71671978, 0.00627995, 0.30814461,
0.72897845, 0.51545988, 0.57818907, 0.69467508, 0.42554708])
print(ex2.min())
print(np.quantile(ex2,0.25))
print(np.median(ex2))
print(np.quantile(ex2,0.75))
print(np.max(ex2))
0.006279953666841864 0.27187609181029326 0.47050348192359215 0.6655535802201438 0.7289784495557392
If you are familiar with Python's standard list indexing, indexing in NumPy will feel quite familiar. It offers several ways to index into arrays.
In a one-dimensional array, the value (counting from zero) can be accessed by specifying the desired index in square brackets, just as with Python lists:

And you can index and slice numpy arrays in multiple dimensions. If slicing an array with more than one dimension, you should specify a slice for each dimension using a comma-separated tuple of indices:
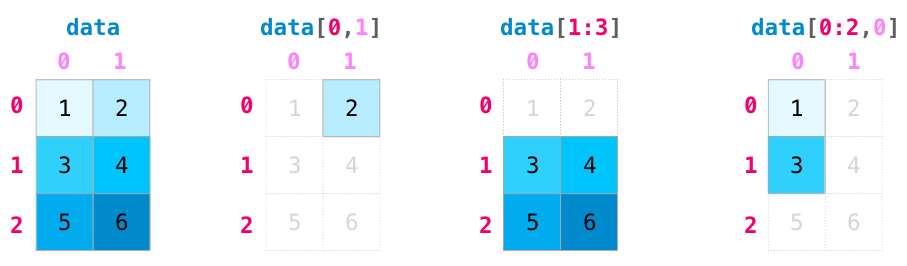
x1 = np.random.random(10) #create one dimensional array
x1
array([0.84473521, 0.25480532, 0.04202275, 0.97207065, 0.17375351,
0.76710637, 0.48383864, 0.51858609, 0.64259706, 0.54944136])
x1[0]
0.8447352143549912
x1[4]
0.17375350556132374
x1[0:2]
array([0.84473521, 0.25480532])
x1[len(x1)-1] #the accessing the last entry
0.5494413589911319
Alternatively, you can use negative indices to index from the end of the array.
x1[-1]
0.5494413589911319
x1[-2]
0.6425970578161072
As stated above, you can use comma seperated tupples for multidimensional array.
# Create the following rank 2 array with shape (3, 4)
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
a
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
# Use slicing to pull out the subarray showing the first entry
a[0,0]
1
# Use slicing to pull out the subarray showng the (2,3)^th element of the array
a[1,2]
7
Two ways of accessing the data in the middle row of the array. Mixing integer indexing with slices yields an array of lower rank, while using only slices yields an array of the same rank as the original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
row_r3 = a[[1], :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape)
print(row_r2, row_r2.shape)
print(row_r3, row_r3.shape)
[5 6 7 8] (4,) [[5 6 7 8]] (1, 4) [[5 6 7 8]] (1, 4)
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape)
print()
print(col_r2, col_r2.shape)
[ 2 6 10] (3,) [[ 2] [ 6] [10]] (3, 1)
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
print(b)
[[2 3] [6 7]]
Integer array indexing: When you index into numpy arrays using slicing, the resulting array view will always be a subarray of the original array. In contrast, integer array indexing allows you to construct arbitrary arrays using the data from another array. Here is an example:
a = np.array([[1,2], [3, 4], [5, 6]])
a
array([[1, 2],
[3, 4],
[5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]])
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]]))
[1 4 5] [1 4 5]
a = np.arange(0,10,1)
a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
a) Pull out the second element.
a[1]
1
b) Pull out the first 5 elements
a[0:5]
array([0, 1, 2, 3, 4])
ex_32 = np.array([[12, 5, 2],
[ 7, 6, 8]])
ex_32
array([[12, 5, 2],
[ 7, 6, 8]])
a) Shows the third column of the array
ex_32[:,2]
array([2, 8])
b) Shows all rows and first two columns
ex_32[:,0:2]
array([[12, 5],
[ 7, 6]])
A slice of an array is a view into the same data, so modifying it will modify the original array.
print(a[0, 1])
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1])
2 2
a = np.array([3,4,5])
a
array([3, 4, 5])
a[1] = 121342141
a
array([ 3, 121342141, 5])
Consider the 2D array in Exercise 3.2
ex_32 = np.array([[12, 5, 2],
[ 7, 6, 8]])
ex_32
array([[12, 5, 2],
[ 7, 6, 8]])
a) Replace the first element of the array by 3
ex_32[0,0] = 3
ex_32
array([[3, 5, 2],
[7, 6, 8]])
b) Replace the second row by [1,6,5]
ex_32[1,:] = np.array([1,6,5])
ex_32
array([[3, 5, 2],
[1, 6, 5]])
Boolean array indexing: Boolean array indexing lets you pick out arbitrary elements of an array. Frequently this type of indexing is used to select the elements of an array that satisfy some condition. Here is an example:
a = np.array([[1,2], [3, 4], [5, 6]])
a
array([[1, 2],
[3, 4],
[5, 6]])
bool_idx = (a > 2) # Find the elements of a that are bigger than 2;
# this returns a numpy array of Booleans of the same
# shape as a, where each slot of bool_idx tells
# whether that element of a is > 2.
print(bool_idx)
[[False False] [ True True] [ True True]]
# We use boolean array indexing to construct a rank 1 array
# consisting of the elements of a corresponding to the True values
# of bool_idx
print(a[bool_idx])
# We can do all of the above in a single concise statement:
print(a[a > 2])
[3 4 5 6] [3 4 5 6]
bbb = np.random.random(5)
bbb
array([0.93669359, 0.86031809, 0.59110717, 0.06983715, 0.5498046 ])
bbb[bbb>0.4]
array([0.93669359, 0.86031809, 0.59110717, 0.5498046 ])
Create a 1D array by executing the given code.
data = np.array([0.59910553,0.19892384,0.42800147,0.67696757,0.34828451,0.69517928,
0.13703289,0.51119015,0.48787451,0.57731085,0.23286820,0.41338543,
0.65633721,1.35069021,0.12212476,0.47460029,0.26618002,1.20542218,
0.71538627,0.20428730,0.13221638,0.56680370,0.32725263,0.29339787,
0.07488558,0.51300380,0.08008302,0.14898439,1.71885703,0.09566642,
0.85223586,0.45847046,0.23882542,0.41942143,0.54160489,0.48413253,
0.62215659,1.83152943,0.10104083,0.92777223,0.25699445,0.22967180,
0.40207172,0.13048873,0.36742793,0.28115245,1.95182640,1.61350926,
0.57133538,0.20487397])
Determine whether data has outlier or not using 1.5 IQR rule.
Answer:
q1 = np.quantile(data,0.25)
q3 = np.quantile(data,0.75)
iqr = q3-q1
upper = q3 + 1.5*iqr
lower = q1 - 1.5*iqr
data[np.logical_or(data<lower, data>upper)]
array([1.35069021, 1.20542218, 1.71885703, 1.83152943, 1.9518264 ,
1.61350926])
take and put
np.take takes elements from an array along an axis.
a = np.array([4, 3, 5, 7, 6, 8])
indices = [0, 1, 4]
np.take(a, indices)
array([4, 3, 6])
a[[0, 1, 4]]
array([4, 3, 6])
For multi-dimensional arrays, you can use axis argument in function. axis = 0 indicates rows, axis=1 indicates columns for 2D arrays.
b = np.array([[2,6,8],[5,12,17]])
b
array([[ 2, 6, 8],
[ 5, 12, 17]])
np.take(b,[1],axis = 0)
array([[ 5, 12, 17]])
np.take(b,[1],axis = 1)
array([[ 6],
[12]])
np.put replaces specified elements of an array with given values.
a
array([4, 3, 5, 7, 6, 8])
np.put(a, [0], 189)
a
array([189, 3, 5, 7, 6, 8])
a[0] = 189
Apart from computing mathematical functions using arrays and indexing & slicing, we frequently need to reshape or otherwise manipulate data in arrays. The simplest example of this type of operation is transposing a matrix; to transpose a matrix, simply use the T attribute of an array object.
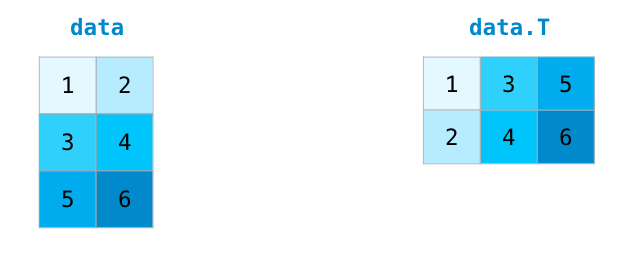
x = np.array([[1, 2], [3, 4], [5, 6]])
print(x)
print("transpose\n", x.T)
[[1 2] [3 4] [5 6]] transpose [[1 3 5] [2 4 6]]
v = np.array([[1,2,3]])
print(v )
print("transpose\n", v.T)
[[1 2 3]] transpose [[1] [2] [3]]
In more advanced use case, you may find yourself needing to change the
dimensions of a certain matrix. This is often the case in machine
learning applications where a certain model expects a certain shape for
the inputs that is different from your dataset. numpy's reshape()
method is useful in these cases.
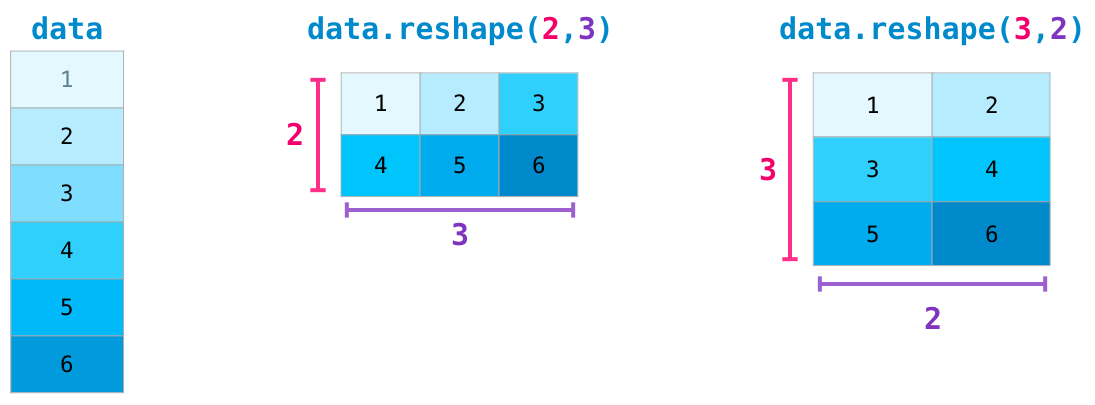
A common task in this class will be to convert a 1D array to a 2D array,
and vice versa. We can use reshape() for this.
For example, suppose we had this 2D array, but we need to pass it to a function that expects a 1D array.
w = np.array([[1],[2],[3]])
print(w)
w.shape
[[1] [2] [3]]
(3, 1)
We can remove the “unnecessary” extra dimension with
y = w.reshape(-1,)
print(y)
y.shape
[1 2 3]
(3,)
Note that we can pass -1 as one dimension and numpy will infer the correct size based on our matrix size!
There’s also a squeeze() function that removes all of the
“unnecessary” dimensions (dimensions that have size 1) from an array:
z = w.squeeze()
print(z)
z.shape
[1 2 3]
(3,)
To go from a 1D to 2D array, we can just add in another dimension of size 1:
y.reshape((-1,1))
array([[1],
[2],
[3]])
Another common task is to combine multiple arrays and create one array. concatenate() function essentially combines NumPy arrays together
x=np.array([[1,2],[3,4]])
y=np.array([[12,30]])
print(x)
print(y)
[[1 2] [3 4]] [[12 30]]
z=np.concatenate((x,y))
z
array([[ 1, 2],
[ 3, 4],
[12, 30]])
x=np.array([[1,2],[3,4]])
y=np.array([[12,30]])
z=np.concatenate((x,y), axis=0)
z
array([[ 1, 2],
[ 3, 4],
[12, 30]])
x=np.array([[1,2],[3,4]])
y=np.array([[12],[30]])
x
y
array([[12],
[30]])
z=np.concatenate((x,y), axis=1)
z
array([[ 1, 2, 12],
[ 3, 4, 30]])
x=np.array([[1,2],[3,4]])
y=np.array([[12,30]])
z=np.concatenate((x,y.T), axis=1) #take the transpose to create a column array
z
array([[ 1, 2, 12],
[ 3, 4, 30]])
Write a NumPy program to create to concatenate two given arrays of shape (2, 2) and (2,1).
You are free to select the elements.
Answer:
Extra
You can generate integers randomly.
np.random.randint(1,5,2) #(min,max,size)
array([3, 1])
np.random.randint(3,15,4) #(min,max,size)
array([13, 14, 13, 14])
You can generate same random numbers by using seed. You can write any number in the seed.
np.random.seed(456)
np.random.random(5)
array([0.24875591, 0.16306678, 0.78364326, 0.80852339, 0.62562843])
np.random.random(5)
array([0.60411363, 0.8857019 , 0.75911747, 0.18110506, 0.15016932])
np.random.seed(456)
np.random.random(5)
array([0.24875591, 0.16306678, 0.78364326, 0.80852339, 0.62562843])
Please open a new notebook.
Create the following arrays.
x = [3 , 4.4, 5.8, 7.2, 8.6, 10]
y = [14.39, 20.14, 25.46, 31.53, 36.67,42.55]
a) Calculate the mean of x
b) Calculate the median of y
c) Calculate the correlation between x and y
d) Concatenate the x and y as a array with shape (2,6)
Download your notebook as .ipnyb file, and send it to metustat112@gmail.com